Container With Most Water

question

给你 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

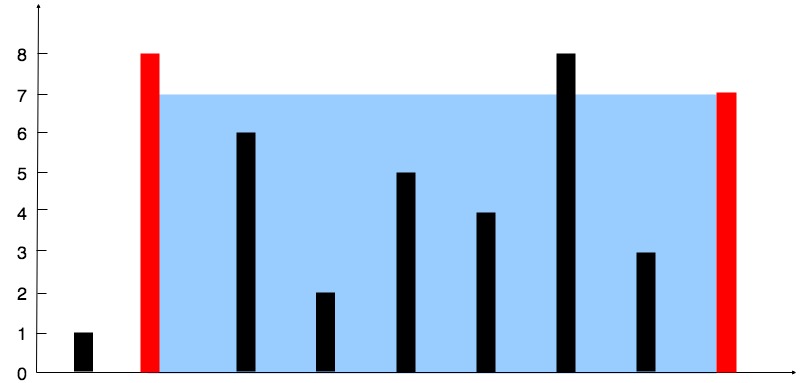
示例：

输入：[1,8,6,2,5,4,8,3,7]
输出：49

tag

Array Two Pointers

my answer

First

• 思路: 暴力解法，直接遍历所有的柱子和其他柱子，记录他们的【最大容量】

public int maxArea(int[] height) {

    int maxWater = 0;
    for (int i = 0;i < height.length - 1;i++) {
        for (int j = i + 1; j < height.length;j++) {
            //这里参考了别人的写法 不用if else来判断两个柱子的最小长度
            int h = Math.min(height[i], height[j]);
            if(h * (j-i) > maxWater){
                maxWater = h * (j-i);
            }
        }
    }
    return maxWater;
}

时间复杂度为O(n2)

Second

大佬的分析nettee

感谢大佬，讲得特别清楚

这道题目看似简单，做起来才发现不容易。分治法、动态规划都用不上，要想得到O(n) 的解法只有使用 双指针 一条路。

即使看了答案知道了双指针解法，你也可能并不清楚这个解法为什么正确。为什么双指针往中间移动时，不会漏掉某些情况呢？

如果没有真正理解题目，即使一次对着答案做出来了，再次遇到这个题目，还是可能做不出来。要理解这道题的正确性和原理，需要从背后的 【缩减搜索空间】的思想去考虑题解。下面我将用图片解释这道题的正确性和原理。

双指针解法的正确性

用一句话概括双指针解法的要点：指针每一次移动，都意味着排除掉了一个柱子。

如下图所示，在一开始，我们考虑相距最远的两个柱子所能容纳水的面积。水的宽度是两根柱子之间的距离 d = 8；水的高度取决于两根柱子之间较短的那个，即左边柱子的高度 h = 3。水的面积就是3×8=24。

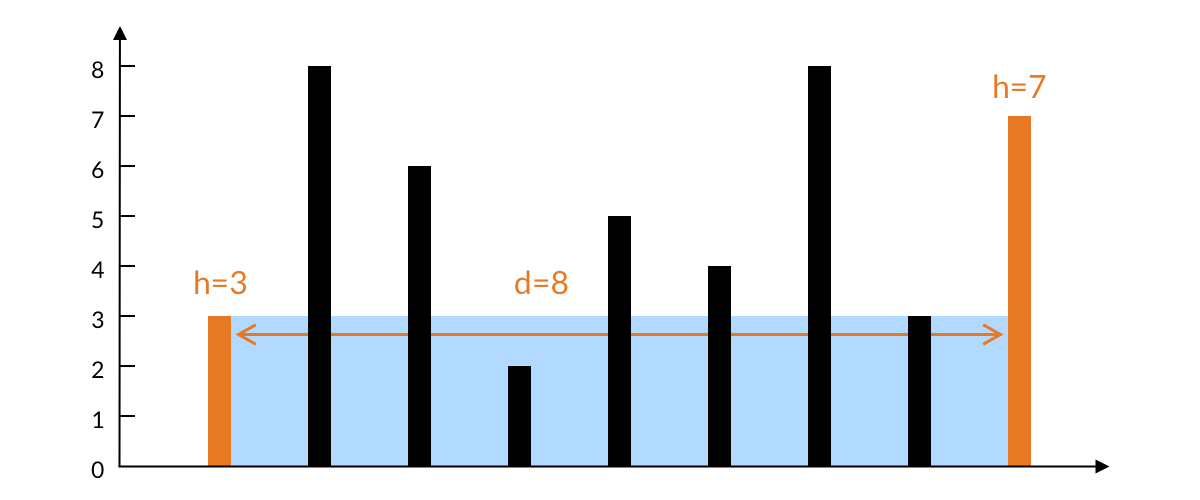
如果选择固定一根柱子，另外一根变化，水的面积会有什么变化吗？稍加思考我们可以确定这么几件事：

• 当前柱子是最两侧的柱子，水的宽度 d 为最大，其他的组合，水的宽度都比这个小。
• 左边柱子较短，决定了水的高度为3。如果移动左边的柱子，新的水面高度不确定，一定不会超过右边的柱子高度 7。
• 如果移动右边的柱子，新的水面高度一定不会超过左边的柱子高度3，也就是不会超过现在的水面高度。

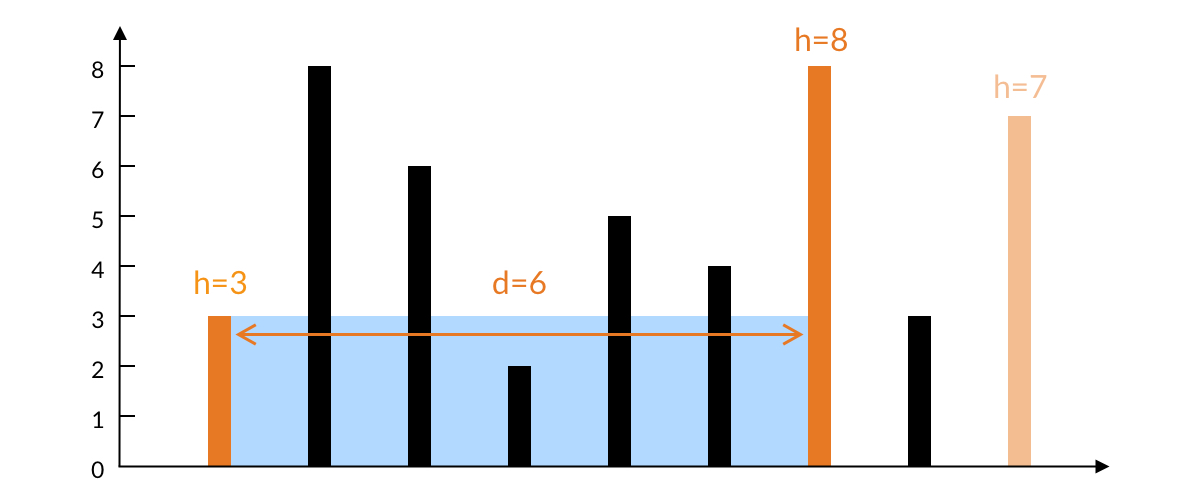
由此可见，如果固定左边的柱子，移动右边的柱子，那么水的高度一定不会增加，且宽度一定减少，所以水的面积一定减少。

这个时候，左边的柱子和任意一个其他柱子的组合，其实都可以排除了。也就是我们可以排除掉左边的柱子了。

这个排除掉左边柱子的操作，就是双指针代码里的 i++。

i 和 j 两个指针中间的区域都是还未排除掉的区域。随着不断的排除，i 和 j 都会往中间移动。当 i 和 j 相遇，算法就结束了。

//自己用java写一遍
public int maxArea(int[] height) {

    int maxWater = 0;

    int i = 0,j = height.length -1;
    while(i < j){
        //计算出当前两个指针位置的最大水面积
        int tmpWater = (j-i) *  Math.min(height[i], height[j]);
        maxWater = Math.max(maxWater,tmpWater);
        //判断移动哪个指针 总是移动短的那根
        //缩减搜索空间
        if(height[i] < height[j]){
            i++;
        }else{
            j--;
        }
    }
    return maxWater;
}

时间复杂度为O(n)

第一遍小结

1. java: 使用一个简洁快速的方法返回两个数中小的那个 Math.min(a,b)

2. 新的思路：双指针、缩减搜索空间